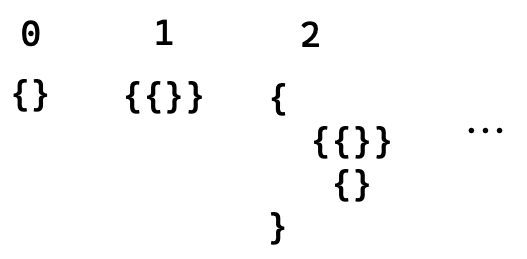[譯]哥德爾的發現(What Gödel Discovered)
本文译自 Stepan Parunashvili 的文章 What Gödel Discovered,已获得作者授权。
本文的目标是向没有接受过严谨逻辑训练的读者提供一种理解不完备性定理的方法,如果你有一定的预备知识,可以直接从 哥德尔的最初想法 一节开始看起。以下是全文:
1931年,25岁的库尔特·哥德尔(Kurt Gödel)写下了一份让数学界天翻地覆的证明。这份证明的意义是如此深远,而他的证明过程却又如此优美——以至于到了有趣的地步。我想要向读者讲述这段发现。需要注意的是,我并不是数学家而是一个程序员,这意味着我的理解是出于直觉,并不精确的。我也希望这会给读者带来一些好处,毕竟我会尽量避免形式化的论证。
统一理论
在过去的300年间,数学家和科学家们做出了无数惊人的发现,它们都指向了一个共有的模式——统一:原本被认为是毫无联系的不同想法最终一致地被发现是单一的,相同的!
牛顿率先为物理学做出了统一:他发现使我们站立在大地上的力量,同时也是牵动地球围绕太阳跳回旋舞的原因;人们本来认为热是一种特殊的能量,之后的发现证实了它同样可以被经典力学表述;人们曾相信电,磁和光都是不同的物质,但麦克斯韦发现它们都可以被同一个电磁场描述。
在生物学方面,达尔文也做了相同的事。我们的下巴、鸟儿美丽的羽翼、可爱的鹿角、形形色色的花卉、雄性和雌性、你如此喜欢糖类的原因以及鲸鱼不同的游动方式,这些都可以被自然选择所解释。
数学家也面临了类似的,为统一而奋斗的道路。他们想要找到的是,能够推导出所有正确理论的数学核心原则。这个原则将能够包容逻辑学,算术和其他数学领域。举个例子,让我们思考这些问题:为什么3小于5?为什么1在2之前?这是毋庸置疑的核心原则(公理)还是可以被更基本的定理导出?自然数是数学的基础概念,抑或是更基本概念的推论?
危机
19世纪,数学家已经在这条道路上取得了巨大的进展。譬如,一个名叫弗雷格(Frege)的绅士发现他可以制造一种集合理论来表示任何东西。他可以用以下的集合来表示数字:
空集表示0,1是包含空集(0)的集合,2则是包含1和0的集合……弗雷格还提供了表示一个数后继的方法:将之前所有自然数都放入同一个集合。更有趣的是,通过这些原理,他可以证明形如”1 + 1 = 2”,”自然数无限”等命题。
这虽然很可怖,也很迷人。这时,伯特兰·罗素(Bertrand Russell)登场了,他只用一击就粉碎了弗雷格的集合大厦。
罗素用弗雷格的理论导出了一个可证却十分荒诞的命题。他证明了形如 1 + 1 = 3(当然这并不十分准确,详情请参阅罗素悖论)的结论。这似乎无关紧要,毕竟仅仅只有一个命题,但它对数学基础的后果,确是灾难性的。如果你能证明 1 + 1 = 3,那你显然不能相信任何从这个基础中导出的真命题了。
这个悖论使数学家们陷入了混乱,他们称这段时期为“第一次数学危机”。
希尔伯特计划
在解决这个问题的努力中,一位名叫希尔伯特(Hilbert)的数学家给出了数学基础所需要满足的一些要求。他认为,这个理论必须是由一系列满足两个主要限制的公理组成的全新数学语言:
这个理论必须能够证明所有真的数学命题。比如说,如果数学基础不能证明 1 + 1 = 2 这个命题,那它一定不能证明所有数学命题。希尔伯特把这条性质称为完备性,也即,数学基础必须是完备的。
第二个硬性要求,就如之前所讨论的:是理论不能证明任何假的数学命题。如果我们能推导出 1 + 1 = 3,那么所有的努力都是徒劳的。希尔伯特把这称为一致性,也即,数学基础必须是一致的。
罗素和怀特海
在弗雷格理论的废墟上,罗素和阿尔弗雷德·诺思·怀特海(Alfred North Whitehead)一起建立了他们自己的理论。他们花费数年时间写下了一本巨著——《数学原理》(Principia Mathematica, 参见SEP)。
他们写下了一种从几条规则导出的新数学语言(我们称它为 PM)。接下来,他们使用这些规则证明了许多东西。罗素和怀特海在一开始几乎没引入任何公理。比如,我们可以一窥这份几乎不可阅读的证明(读者不需要明白论文中的语法):
以上段落证明了,1 + 1 确实等于 2。他们写下了两卷的前置知识来证明这个定理。
这种语言十分严密,使得证明的工作量尤为巨大,但罗素和怀特海依然努力证明了数学中许多不同的真命题,并且在当时,并没有人能够给出反例和发现漏洞。人们甚至设想这项理论可以作为超越数学的基础:我们难道不能用它形式化一只狗的行为,或是人类复杂的思维规律吗?
哥德尔的出现
在哥德尔出现前,似乎我们有理由置信,数学原理会是真正的数学基础。
但哥德尔却证明了,数学原理中确实含有不可证的真命题,也即,数学原理是不完备的。
这还不够,他甚至能够证明希尔伯特计划背后的动机——找到一个数学的形式基础,是不可行的。
这似乎令人难以接受,一个人真的可以证明某些事情绝不可能发生吗?设想有个人告诉你人类永远不可能离开太阳系,你一定会对他的说辞抱有怀疑。
并且当时,哥德尔只有25岁,却无可置疑地证明了这个计划的空想。形式化地讲,他证明了任何一个能够表示自然数的逻辑系统,总存在在那之中不可证的命题。(哥德尔第一不完备性定理)
让我们好好考虑一下上面的表述:自然数似乎很直觉化地容易表述:只是些1,2,3等等……人们相信他们可以逐步写下所有自然数和衍生的定理。因此,当他们听说甚至连自然数的所有事实都不能被证明时,该有多么震惊了。
接下来,我们来看看哥德尔的推理过程。
PM-Lisp
既然罗素和怀特海的语言是如此难以阅读,我们不妨改变一些他们的符号。让我们来将他们的形式语言转换为一些对程序员更亲切的东西:Lisp!
你可以想象罗素发明了一种与 Lisp 类似的编程语言,它的语法如下:
首先,这门语言有一些算术符号。
| 符号 | 意义 | 例子 |
|---|---|---|
| 0 | 零 | 0 |
| next | 后继 | (next 0) |
| + | 加 | (+ 0 (next 0)) |
| * | 乘 | (* 0 (next 0)) |
| = | 等于 | (= 0 (* 0 (next 0))) |
这些符号已经足够表示任何自然数,符号 0 就是自然数的开始,符号 next 则是一个后继函数,那么 (next 0) 就可以表示1, (next (next 0)) 就是2,依此类推。
我们可以这么表述 1 + 1 = 2 :
(= (+ (next 0) (next 0))
(next (next 0)))
现在,为了这篇文章的论述方便,我需要添加额外的一条规则。如果你看到我在 PM-Lisp 中写下一个不同于0的自然数(如15),你可以认为是 (next (next (next ...))) 的缩写。也即,将 next 函数作用于0上15次得到15。
| 符号 | 意义 | 例子 |
|---|---|---|
<natural-number> |
(next (next ...)) 作用于 0 <natual-number> 次 |
3 means (next (next (next 0))) |
(next (如上)),他们定义了一些表述逻辑的符号:
| 符号 | 意义 | 例子 |
|---|---|---|
| not | 非 | (not (= 0 1)) |
| or | 或 | (or (= 0 1) (not (= 0 1))) |
| when | 蕴含 | (when 0 (or 0 1)) when 0, then there is either 0 or 1 |
| there-is | 存在……使得…… | (there-is x (= 4 (* x 2)) |
这些符号和我们在编程中使用的逻辑词是一致的。比较不同的是 there-is,我们来举个例子。
(there-is x (= 4 (* x 2)))
该语句表述了一个命题,存在一个数 x ,使得 (* x 2) 等于4。显然这是正确的:x=2。我们现在可以表述出普遍化的算术命题了。
那 x 又是从哪里来的呢?我们需要添加这些东西到我们的语言中来:
| 符号 | 意义 |
|---|---|
| a…z, A…Z | 变量 |
为了能够表述普遍真理,罗素和怀特海引入了符号,我们可以使用 and 的推导过程作为一个例子:
(not (or (not A) (not B)))
当该命题为真时,A 与 B 一定都是真的。
接下来是最后一个小技巧,为了更方便阅读,有时我们可以引入新的符号。它们并不是该语言的一部分,仅仅是作为这篇文章中出现的缩写。
| 形式 | 意义 | 例子 |
|---|---|---|
(def <name> <formula>) |
定义 <name> 为 <formula> |
(def and (not (or (not A) (not B))) same as (and <var-a> <var-b>...) |
现在我们就可以写下 (and 1 2) 了。🙂
PM-Lisp 的公理
我们目前看到的都只是些符号,它们还没有任何意义。
罗素和怀特海需要证明 0 确实是零,而 = 也确实是相等的意思。为了给符号赋予生命,他们从一系列核心原则——公理集开始。
以下是他们选取的公理:
| 公理 | 例子 |
|---|---|
(when (or p p) p) |
若苹果或苹果,则苹果 |
(when p (or p q)) |
若苹果,则苹果或香蕉 |
(when (or p q) (or q p)) |
若苹果或香蕉,则香蕉或苹果 |
(when (or p (or q r)) (or q (or p r)) |
若梨或苹果或香蕉,则苹果或梨或香蕉 |
(when (when q r) (when (or p q) (or p r)) |
若苹果是水果,且苹果或香蕉,则水果或香蕉 |
这便是全部公理,是我们需要相信的所有东西。他们使用这些规则,不厌其烦地组合它们,组成其余一切的错综复杂的证明。
比如,他们定义 = 为:
(def = (and (when A B) (when B A)))
若 A 蕴含 B,且 B 蕴含 A,则它们一定相等。想象一下,他们用了数百页推出这个定义。
这里需要特别注意的是:他们的规则十分精确以至没有给人类解释的余地,计算机可以运行这些规则,这便是数学基础的关键所在:如果这些规则判断简单到可以被表述为一个算法,我们就能去除人工检查的额外错误。
哥德尔的最初想法
现在,哥德尔想要来研究罗素和怀特海的形式语言。但是符号是很难被研究的,我们无法推理符号之间的关系。
但是,确实存在着一样可以被方便研究的东西——自然数!所以哥德尔想出了这样一个主意:如果他能够把整个 PM-Lisp 都用自然数表示呢?
这便是他所做的最初工作。
符号
首先,他给所有的符号赋值:
| 符号 | 哥德尔数 |
|---|---|
| ( | 1 |
| ) | 3 |
| 0 | 5 |
| next | 7 |
| + | 9 |
| * | 11 |
| = | 13 |
| not | 15 |
| or | 17 |
| when | 19 |
| there-is | 21 |
| a | 2 |
| b | 4 |
| c | 6 |
| … | … |
现在,如果他想要写 when ,他可以只写19。然而这并不足够:我们怎么表示公式呢?
公式
哥德尔为表示公式也创建了一种方法,他使用一条规则:
将任何公式,比如:
(there-is a (= (next 0) a))
先转换为每个符号对应的哥德尔数:
| 符号 | ( | there-is | a | ( | = | ( | next | 0 | ) | a | ) | ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 哥德尔数 | 1 | 21 | 2 | 1 | 13 | 1 | 7 | 5 | 3 | 2 | 3 | 3 |
然后他使用递增的素数列,将每一个哥德尔数作为其中素数的幂:
| 素数^哥德尔数^ | 2¹ | 3²¹ | 5² | 7¹ | 11¹³ | 13¹ | 17⁷ | 19⁵ | 23³ | 29² | 31³ | 37³ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
将它们相乘,得到一个巨大的自然数:
25777622821258399946386094792423028037950734506637287219050
这是个十分有趣的数,因为它是递增素因子的乘积,这保证了它是唯一的。这也就意味着,每一个 PM-Lisp 中的公式都可以被唯一的哥德尔数表示。
证明
公式并不是 PM-Lisp 的全部,我们仍然需要支持书写证明,证明是一系列的公式:
(there-is a (= (next 0) a))
(there-is a (= a (next 0)))
哥德尔用了和上一节一样的技巧,将每一个公式转换为哥德尔数:
| 公式 | (there-is a (= (next 0) a)) |
(there-is a (= a (next 0))) |
|---|---|---|
| 哥德尔数 | 25777622821258399946386094792423028037950734506637287219050 | 76887114166817775146256448336954145299389470803180389491850 |
| 素数^哥德尔数^ | 225777622821258399946386094792423028037950734506637287219050 | 376887114166817775146256448336954145299389470803180389491850 |
然后
2^25777622821258399946386094792423028037950734506637287219050 * 3^76887114166817775146256448336954145299389470803180389491850
这是一个天文数字,仅仅是算式的第一项就有七十亿亿项数字,但是我们的确得到了想要的结果——这个天文数字独一无二地表示了以上的证明。
现在,我们可以用哥德尔数唯一编码符号,公式,甚至证明了。
PM-Lisp 上的 PM-Lisp
我们已经可以用数学来研究自然数:比如“偶数和素数间有什么关系?”,“素数是否无限多?”等等。哥德尔意识到他可以使用与研究素数一样的方法来研究所有代表 PM-Lisp 证明的数字。
那么,哥德尔该用什么形式语言来研究这些数字呢?罗素和怀特海确保了 PM-Lisp 适用于研究自然数,那么显然它一定适用于研究素数。所以我们为什么不适用 PM-Lisp 来研究所有代表 PM-Lisp 证明的数呢?
这正是哥德尔下一步做的:他用 PM-Lisp 研究了 PM-Lisp。
这当然不是罗素和怀特海原本的用意,但它确实是合理的行为。接下来,我们使用一些例子来理解这个概念。
描述公式
我们有以下公式:
(there-is a (= (next 0) a))
我们怎么证明定理“该公式的第二项是 there-is” 呢?
该公式的哥德尔数如下:
25777622821258399946386094792423028037950734506637287219050
以上命题就被转换成了:
“该哥德尔数中最大可以被 3 整除的因子是 3^21^ 。”
这个关系在 PM-Lisp 中就容易描述多了,我们来写一个描述一个数是另一个数因子的公式:
(there-is x (= (* x 5) 30))
这个命题的意思是,存在 x 使得 (* x 5) 等于 30。x = 6 是使这个命题为真的解,因此,5确实是30的一个因子。我们可以定义如下的判断因子的函数:
(def factor? (there-is x (= (* x y) z)))
本节最初的命题可以用以下公式描述:
(and
(factor? x 3^21 25777622821258399946386094792423028037950734506637287219050)
(not (factor? x 3^22 25777622821258399946386094792423028037950734506637287219050)))
这个命题的意思是,3^21^是这个数的因子,而3^22^不是。如果该命题为真,就意味着3^21^的确是 25777622821258399946386094792423028037950734506637287219050 中最大能被3整除的因子。这也就意味着,原公式的第二项确实是 there-is。(Mathematica 告诉我们这是真的)
创造公式
更进一步的,我们甚至能在 PM-Lisp 中创造出新的 PM-Lisp 公式!我们有如下的关于指数和素数的辅助命题:
(def prime? ...) ; (prime? 5) ; true
(def largest-prime ...) ; (largest-prime 21) ; 7
(def next-prime ...) ; (next-prime 7) ; 11
(def expt ...) ; (expt 10 3) ; 1000
罗素和怀特海当然也可以用他们的形式语言定义以上的命题,接着,我们就可以写一个给 PM-Lisp 公式续上一个 “)” 的公式:
(* n (expt (next-prime (largest-prime n)) 3))
如果 n 是表示 (there-is a (= (next 0) a)) 的哥德尔数,
这个公式的意思就是:
- 找到
n中最大的素数:37 - 得到下一个素数:41
- 将
n乘上 41^3^
这等价于给原公式结尾附上一个新的 “)”。是不是略有些难以理解?
(successor? a b)
接下来,哥德尔好奇的是,我们还能创造其他有趣的命题吗?我们能写下如下的命题吗?
(successor? a b)
这个命题的意思是:哥德尔数 a 表示的公式可以推导出公式 b 。
这确实是一个 PM-Lisp 中可证的合理命题。它的数学证明过程比较繁琐,我们可以只阐述思路。
在 PM-Lisp 中,要从一个公式出发到达另一个公式,我们必须以罗素和怀特海给出的公理为依据。
例如,我们可以从命题 p 根据公理 (when p (or p q)) 推出 (or p q)。然后我们再依据公理 (when (or p q) (or q p) 转换到 (or q p),如此等等。
我们已经知道,PM-Lisp 可以在公式两侧添加新的符号(比如上节我们在结尾处添加的 ))。一些更加复杂的命题也可以帮助我们根据已有公理和命题,组合出新的命题。例如我们要从 p 到 (or p q) ,需要一个接受 p 的哥德尔数,返回在之前添加上 (or ,之后加上 q) 后的哥德尔数的数学函数。
数论中的一些理论为以上的设想奠定了基础,我们略过这些过程,直接写下检查某命题是否是一系列命题合理后继的公式:
(def successor?
(one-of b (possible-successors a)))
这个定义检查从 a 出发的所有可能公式中,是否有一个与 b 相等,如果为真,那 b 就是 a 的后继。
好!现在 PM-Lisp 已经可以言说一个命题是否蕴含另一个了。
(proves a b)
下一步是命题 (proves a b)。它的意思是:哥德尔数 a 代表的证明过程可以证明哥德尔数 b 表示的命题。
我们好好考虑一下,从哥德尔数 a 还原出证明序列是十分容易的,只需要分解出每个素数的指数,PM-Lisp 可以轻松地处理这项工作。
我们已经有一个 successor? 函数了,只需要将其作用于分解出的每一对命题,确保它们是合法的即可。
(and
(every-pair sucessor? (extract-sequence a))
(successor? (last-formula a) b))
在这里我做了很多没有详细说的抽象—— every-pair 和 extract-sequence 等等,但是读者可以明白,这些抽象过程都是一个复杂的数学函数,它们分解出一个证明序列并把它们组合成有序对。
以上的命题有力地证明了:
哥德尔数 a 代表的公式序列中每一个成员都是合法的后继,并最终蕴含了哥德尔数 b。
哥德尔在他的论文中费了很大功夫证明这项命题,对我们来说,只需要明白其中的直觉推理就足够了。我们现在可以使用 PM-Lisp 来表述许多非平凡的关于 PM-Lisp 的事实了,比如“对该命题的证明是有效的”。这非常酷!
(subst a b c)
这是哥德尔证明的最后一步,想想我们有如下公式:
(there-is b (= b (next a)))
它的哥德尔数是
26699108848097731568417316859014651425159900891216992323750
它的意义是:存在一个数 b 是 a 的后继。
现在,如果我们需要将符号 a 替换为 0 该怎么办呢?
这是一件艰难却很直接的事情:我们只要将哥德尔数中所有指数2替换成5即可(回忆一下,2是 a 的哥德尔数,5是0的哥德尔数)。
(replace-exponent
26699108848097731568417316859014651425159900891216992323750
2
5)
这是很直截了当的数学计算,PM-Lisp 能够做到,尽管它有很多繁琐的过程,提取指数,执行乘法,但确实是在逻辑允许的范围之内的。
哥德尔证明了这个函数在 PM-Lisp 中是可证命题,我们上述的表达式可以产生以下公式:
(there-is b (= b (next 0)))
很好,我们成功将 a 都替换成了 0,我想罗素和怀特海看到这些举动,可能会十分不解甚至排斥。
subst 的可疑之处
如果他们没有觉得上述举动令人排斥的话,接下来要做的绝对会更进一步:
(subst
26699108848097731568417316859014651425159900891216992323750
4
26699108848097731568417316859014651425159900891216992323750)
这个公式将 a 替换成了哥德尔数本身!
因此,我们就会有如下公式:
(there-is b (= b (next 25777622821258399946386094792423028037950734506637287219050)))
在一个公式中使用代表本身的哥德尔数十分奇怪,但既然它只是一个稀松平常的自然数,这一切都是合乎逻辑的。
我们来总结一下,PM-Lisp 现在可以检验一个证明是否合理,甚至可以替换公式中的任意符号了!
点睛之笔
哥德尔用上述公式谱写了一曲伟大的合奏:
首先我们有:
(proves a b)
意味着:哥德尔数 a 代表的证明序列可以证明公式 b。
接下来,他添加了一个 there-is
(there-is a (proves a b))
意味着:存在一个公式 b 的证明 a。
然后,他又加上了 not:
(not (there-is a (proves a b)))
意味着:不存在公式 b 的证明。
接着,他使用了 subst:
(not (there-is a (proves a (subst b 4 b))))
好吧,如果一定要说的话,这个公式的意思是:
不存在将公式 b 中的符号 b(4是符号 b 的哥德尔数) 替换成代表公式 b 的哥德尔数获得的新公式的证明。
b 是什么?既然它是个符号,它就可以表示任何东西,现在我们给它赋予一个特定的值。定义公式
(not (there-is a (proves a (subst b 4 b))))
的哥德尔数为 G (显然它非常大),我们将上述公式中的 b 都替换为 G。
(not (there-is a (proves a (subst G 4 G))))
非常有趣,这个公式的意思又是什么呢?
哥德尔公式
我们再仔细审视它一遍:
(not (there-is a (proves a (subst G 4 G))))
它的意思是:不存在将公式
(not (there-is a (proves a (subst b 4 b))))
中的 b 替换为该公式本身的哥德尔数 G 得到的新公式
(not (there-is a (proves a (subst G 4 G))))
的证明。
等一下!这不就是我们最开始的公式吗?
这似乎意味着公式
(not (there-is a (proves a (subst G 4 G))))
本身在说:“我在 PM-Lisp 里是不可证的”😮
该相信什么?
这是个有趣的命题,它是真的吗?我们仔细思考:
“上式在 PM-Lisp 中不可证” 若是真的,也就意味着 PM-Lisp 是不完备的:这个真的数学命题本身在 PM-Lisp 中是不可证的。
如果它是假的,也就意味着 PM-Lisp 能够证明 “上式在 PM-Lisp 中不可证”。但是,如果这个命题可以被证明,它一定是假的!既然这个命题可以被证明是正确的,它怎么能是不可证明的呢?所以这意味着 PM-Lisp 是不一致的 —— 它推出了一个形如 1 + 1 = 3 的假命题。
因此哥德尔得到了以下令人震惊的结论:如果 PM-Lisp 一致,那它一定不完备,如果它完备,那它一定不一致。
自然数的力量
这对罗素和怀特海显然是一个打击,但这如何与希尔伯特的计划相关呢?我们能不能想出一个新的形式语言避免这个悖论?
但是我们注意到,只要这门新语言能够表示全部自然数,它就会掉入同样的逻辑陷阱:哥德尔可以很轻松的将这门新语言映射为自然数,然后使用新的 successor? 函数来产生等价的不可证命题。
他打破了许多数学家的美梦:即使是最简单的一阶算术都存在不能被完全公理化的局限。在编程中,这个命题的等价表述就是:存在一些永远不能被算法形式化的事实。这便是哥德尔发现的重要意义。
他在随后一年还证明了更加有趣的结论(哥德尔第二不完备):他可以写下一个相类似的,不能证明自身一致性的命题。这意味着没有形式系统可以在自身范畴内证明其一致性。

但这并不意味着我们所做的一切都是徒劳的。例如,不完备定理也许意味着我们不能写出模拟狗思考的算法……但也许我们并不需要写出这个算法。就像神经元不知道狗爱玩玩具一样,我们的算法也不必如此:也许意识本身会用相同的方式演化出该现象。”像狗一样思考 “的想法只是不能被具体地写下来而已。
我们不能在一个系统中证明它的一致性,但我们可以在另一个系统中证明。当然这带来了其他问题:另一个系统的一致性怎么证明?如此等等!
我认为哥德尔的定理起到了一个指导作用:它呈现了我们使用既定算法的局限性。我也发现哥德尔所做的带有一丝戏谑:罗素和怀特海花了极大的精力避免在他们的系统中出现自我指涉和循环论证,哥德尔却使用首创的“自循环解释器”(一门解释它本身的语言,如 Lisp)巧妙地绕过了这些麻烦,从而证明了许多惊人的事实。
结语
我希望你能在这篇文章中得到一些乐趣 :)。如果你想要深入探究哥德尔的证明,你可以参考这几本书籍。Hofstadter 的 “I’m a Strange Loop” 在第九章给了个简短的介绍。Nagel 和 Newman 的 “Gödel’s Proof” 详细介绍了背景和对当时学界有条理的回顾。更进一步地,我非常推荐阅读 Peter Smith 的 “Introduction to Gödel’s Theorems”。他给出了 (proves a b) 和 (subst a b c) 非常详尽的证明。
最后,如果你想要构造你自己的哥德尔数,这里有一个 Clojure 写的脚本。